| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | |||
| 5 | 6 | 7 | 8 | 9 | 10 | 11 |
| 12 | 13 | 14 | 15 | 16 | 17 | 18 |
| 19 | 20 | 21 | 22 | 23 | 24 | 25 |
| 26 | 27 | 28 | 29 | 30 | 31 |
- 개발일지
- jpa
- 만다라트프로젝트
- 자바
- 유학생 준비물
- JVM아키텍처
- 개인 프로젝트 개발일지
- 케네스
- 해외유학
- Java 스터디
- California State University Sacramento
- 미국유학생
- 유학생대학생활
- 사이드프로젝트
- java
- F1학생비자
- i-20
- 케네스로그
- 비전공자 git
- 미국대학
- 미국대학생활
- CSUS
- 파이데이아창의인재학과
- 미국유학생활
- 자바 스터디
- 2+2
- Kenneth Park
- 미국유학
- 복수학위제도
- 부산외대
- Today
- Total
케네스로그
[자료구조/Java] Heap 힙 본문

힙(heap)은 데이터에서 최대값과 최소값을 빠르게 찾기 위해 고안된 완전 이진 트리(Complete Binary Tree)입니다.
Heap의 특성
- 트리에서 사용되었던 노드가 아닌, Array를 활용하여 데이터를 관리합니다.
- 노드를 삽입하면 배열(트리)의 가장 마지막에 삽입합니다.
- Top에 위치한 최대값/최솟값을 O(1)의 복잡도로 리턴합니다.
- 오직 Parent, Child의 비교 규칙만 준수합니다.
힙과 이진탐색트리의 비교
이진탐색트리는 탐색을 위한 자료구조이며, Heap은 최대/최소값을 탐색하기 위한 자료구조
이전에 이진탐색트리(Binary Search Tree)에서는 부모와 자식간의 관계를 유지하는 것이 트리 형성 규칙이었습니다. 힙에서는 기본적으로 부모가 자식보다 크기만 하면 트리를 유지할 수 있습니다. 왼쪽자식과 오른쪽 자식의 크기 관계는 무관합니다.
최대 힙 Max Heap
최대 힙(Max Heap)은 완전 이진 트리(Complete Binary Tree)로써, 최대값을 탐색하기 위해 존재하는 배열 형태의 자료구조를 말합니다. 최솟값을 찾기 위한 최소 힙(Min Heap)도 존재합니다.
이번 포스팅에서는 Max Heap을 기준으로 설명하도록 하겠습니다.
Max Heap의 인덱스 패턴

힙은 트리의 형태로 시각화 할 수 있지만, 실제론 배열의 형태로 저장됩니다. 배열의 인덱스 번호가 트리의 각 노드를 위와 같이 해당됩니다. 아래는 현재 노드 i를 기준으로 각 노드들의 패턴을 나타낸 것 입니다.
- 현재 노드: i
- 부모 노드: (i-1)/2
- 왼쪽 자식 노드: (i*2)+1
- 오른쪽 자식 노드: (i*2)+2
0번 인덱스가 부모 노드라면, 0의 왼쪽 자식 노드는 (2*0)+1인 1, 오른쪽 자식 노드는 (2*0)+2인 2가 됩니다.
부모 노드가 인덱스 2라면, (2*2)+1=7, (2*2)+2=8, 즉 7과 8이 각 자식노드에 해당되게 됩니다.
Heap의 기본 메소드
- getMax() : Max Heap의 Top 리턴
- extractMax() : root를 제거하고 heapify()를 통한 재정렬
- heapify(): heap의 특성을 유지하기위해 노드 재배치
- insert() : 새로운 데이터를 트리 마지막에 삽입한 후, heapify()를 통한 재정렬
Heap의 삽입 insert
삽입할 노드는 왼쪽 최하단 노드(배열의 끝)부터 채워집니다. 그리고, 부모 노드와 크기를 비교하여 교체합니다. 이러한 과정을 트리의 밸런스가 유지될때까지 반복합니다. 아래의 예시를 통해 삽입과정을 알아보겠습니다.

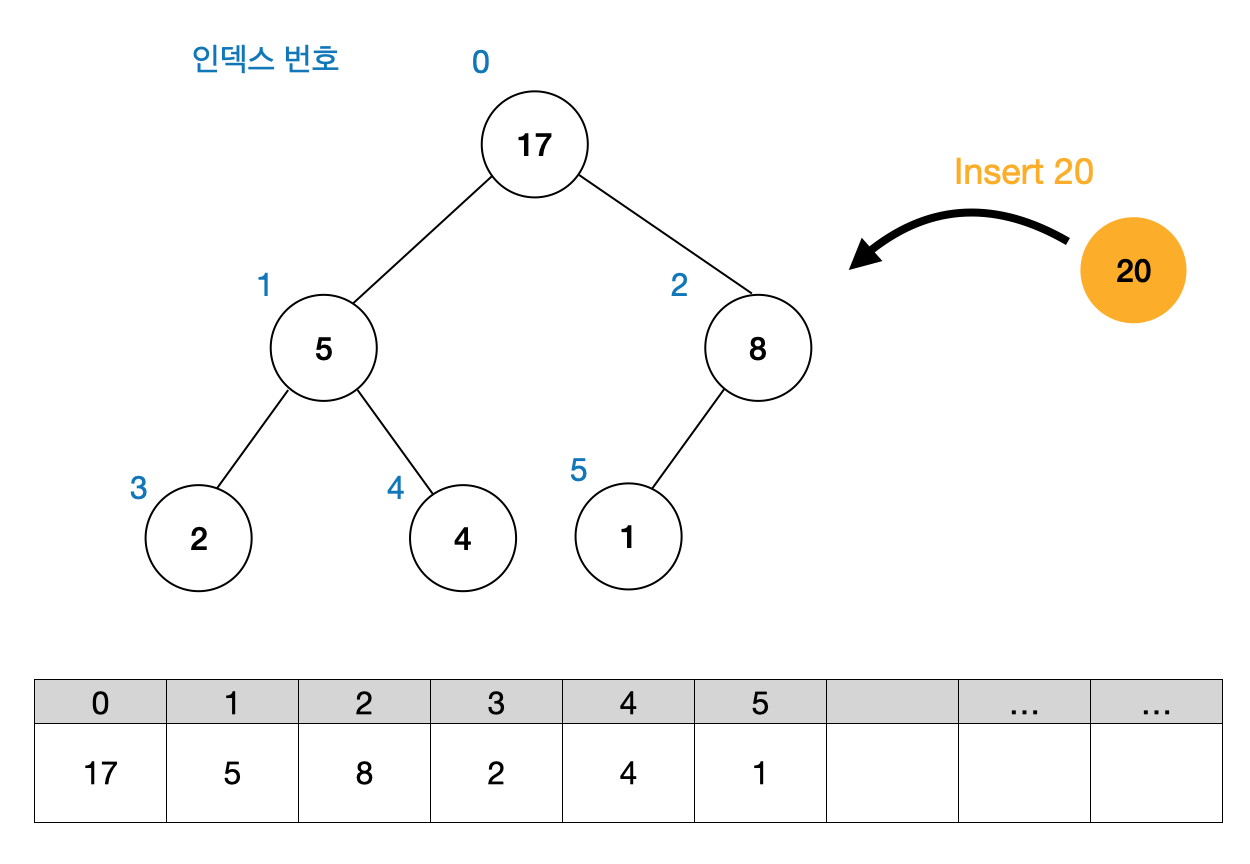





public boolean insert(Integer data) {
int current = this.size; // 7
this.heap.add(data);
this.size++;
// reversed heapify process
// from bottom to top
while (current != 0) {
if(this.heap.get(current) > this.heap.get(this.getParentPos(current))) {
swap(current, this.getParentPos(current));
}
current = this.getParentPos(current);
}
return true;
}
정렬 heapify메소드
Heap에서 삽입, 삭제 등의 과정에서 트리의 규칙을 유지하고 노드를 재정렬하는 메소드를 heapify()라고 합니다. heapify()메소드는 트리의 밸런스가 유지될때까지 반복해서 동작하며, 위치가 변경되어야할 노드가 있다면 swap()메소드를 통해서 변경됩니다. 아래는 heapify()메소드의 전문입니다.
// heapify from top to bottom
public boolean heapify(int pos) {
if (this.isLeaf(pos)) {
return true;
}
// 왼쪽 자식 1개만 남아있는 경우,
// 현재 노드와 왼쪽 자식노드만 비교해서 스왑이 필요한 경우엔 스왑 진행 후 종료
if(this.getRightPos(pos) >= this.size) {
if(this.heap.get(this.getLeftPos(pos)) > this.heap.get(pos)) {
swap(pos, this.getLeftPos(pos));
}
return true;
} else {
// subtree에서 해당 Posisition을 기준으로 좌/우 자식 중 한쪽 이상이 더 크다면,
if(this.heap.get(pos) < this.heap.get(this.getLeftPos(pos)) ||
this.heap.get(pos) < this.heap.get(this.getRightPos(pos)) ) {
// 왼쪽 자식이 오른쪽보다 크다면
if(this.heap.get(this.getLeftPos(pos)) > this.heap.get(this.getRightPos(pos))) {
if(this.heap.get(pos) < this.heap.get(this.getLeftPos(pos)) ) {
// 왼쪽 자식과 부모를 스왑한 후, 왼쪽 자식을 기준으로 다시 heapify
swap(pos,this.getLeftPos(pos));
heapify(this.getLeftPos(pos));
}
} else {
// 왼쪽 자식이 더 크다면
if (this.heap.get(pos) < this.heap.get(this.getRightPos(pos)) ) {
swap(pos, this.getRightPos(pos));
heapify(this.getRightPos(pos));
}
}
}
}
return true;
}MaxHeap 클래스의 자바 소스코드 전문은 깃허브 이곳에서 확인할 수 있습니다.
'Dev > 자료구조' 카테고리의 다른 글
| [자료구조/Java] 이진탐색트리 - 탐색/삽입/삭제 (0) | 2022.01.24 |
|---|---|
| [자료구조/Java] Hash 해시 (0) | 2022.01.21 |
| [자료구조/Java] LinkedList - 조회/추가/삭제 코드구현 (0) | 2022.01.21 |
| [자료구조/Java] Stack (Java구현, 관련 메소드) (0) | 2022.01.02 |
| [자료구조/Java] Queue (Java구현, 관련 메소드) (0) | 2021.12.28 |




